Le Torri di Hanoi (parte 2)

Nel post precedente abbiamo introdotto il gioco delle Torri di Hanoi, che consiste nello spostare un certo numero di dischi di grandezza crescente su tre pioli. Il gioco è risolto quando tutti i dischi vengono trasferiti su un piolo diverso da quello iniziale. E’ un rompicapo non banale, perché il vincolo di dover spostare un disco alla volta impilando sempre i dischi più piccoli sopra a quelli più grandi, ha conseguenze importanti sul numero di mosse da effettuare.

Abbiamo detto che, per risolvere questo enigma, abbiamo bisogno di … barare. Ne vediamo subito il perché.

Usiamo la stessa convenzione del post scorso, numerando i tre pioli in sequenza e i dischi in ordine di diametro crescente. Chiamiamo il disco di diametro più piccolo D1, quello di diametro immediatamente superiore D2 e così via D3, D4 e D5 per gli altri dischi.

Per risolvere il rompicapo andiamo per passi di complessità crescente, cercando di capire se c’è uno schema che possiamo riutilizzare nella sequenza di mosse. Iniziamo dal caso semplicissimo di un solo disco. La soluzione consiste di una sola mossa:

muovi il disco D1 dal piolo 1 al piolo 2

Per sinteticità, applichiamo la semplice convenzione di indicare le mosse con il nome del disco da spostare. I dischi vanno sempre spostati da sinistra a destra sul primo piolo libero. Adottando questa convenzione, la soluzione ad un piolo è costituita da una sola mossa. Indichiamo la sequenza di mosse con S(1):

S(1) = D1

semplicissimo.

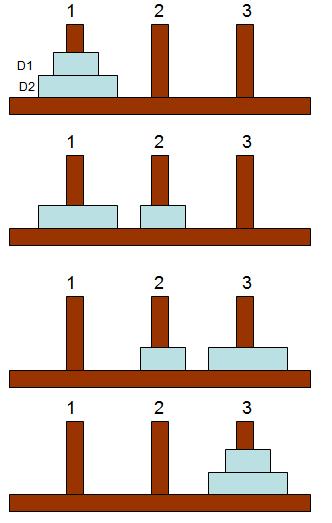
Adesso, risolviamo il rompicapo con 2 dischi, rappresentando la soluzione nella figura seguente allo stesso modo:

S(2) = D1 D2 D1

tre mosse.

Osserviamo adesso una cosa: nella soluzione a 2 dischi abbiamo visto che appare la sequenza di mosse (una sola !) della soluzione ad un disco per 2 volte, cioè possiamo scrivere:

S(2) = S(1) D2 S(1)

Non vi si accende il campanello dell’intuizione ? Abbiamo una soluzione definita in termini di sé stessa, cioè ricorsiva (ne abbiamo già parlato tempo addietro). Ma il risultato che abbiamo trovato sarà valido anche per un numero qualsiasi di dischi ?

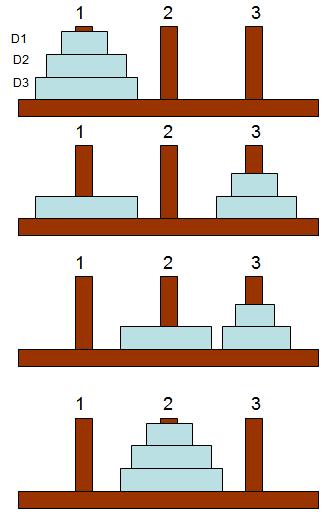Verifichiamolo per 3 dischi (figura a sinistra ). Se bariamo per un attimo, scopriamo che si risolve il problema spostando prima i due dischi D1 e D2, poi il disco D3 e poi nuovamente i dischi D1 e D2. Ma, pensiamoci un attimo, non stiamo affatto barando, perché sappiamo già come si spostano due dischi, è la soluzione S(2) !

Abbiamo appena scoperto che:

S(3) = S(2) D3 S(2)

è la stessa espressione ricorsiva del caso a due dischi.

Per ottenere la soluzione scritta in modo completo, è quindi sufficiente sostituire le espressioni delle soluzioni precedenti per trovare la soluzione a tre dischi:

S(3) = S(2) D3 S(2) = S(1) D2 S(1) D3 S(1) D2 S(1) = D1 D2 D1 D3 D1 D2 D1

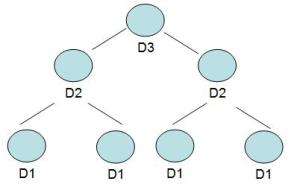
Disegnamo ora graficamente le espansioni delle formule che abbiamo costruito sopra:

lo riconoscete ? E’ un albero binario, ne abbiamo già parlato in un contesto completamente differente.

Abbiamo scritto una soluzione ricorsiva al problema, che per un numero qualsiasi di dischi N è:

S(N) = S(N-1) DN S(N-1)

Quante sono le mosse nel caso generico ? Basta contare il numero di nodi del’albero binario, ma questa è una cosa che sappiamo fare benissimo, lo abbiamo già visto la volta scorsa: il numero di nodi di un albero binario di profondità N è 2^N – 1.

Nel caso di 3 dischi occorrono quindi 7 mosse, nel caso di 5 ne servono 31 e nel caso dei monaci del tempio, impegnati a spostare 64 dischi, occorrono 18.446.744.073.709.551.616 mosse !

Anche spostando un disco al secondo i monaci impiegherebbero la bellezza di 584 miliardi di anni. Possiamo stare tranquilli anche questa volta, il mondo finirà tra tanto, tanto tempo.