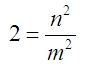 Riprendiamo la dimostrazione iniziata il post precedente. Vogliamo arrivare a dimostrare che radice di 2 è irrazionale attraverso una dimostrazione per assurdo, che usi le proprietà dell’MCD.
Riprendiamo la dimostrazione iniziata il post precedente. Vogliamo arrivare a dimostrare che radice di 2 è irrazionale attraverso una dimostrazione per assurdo, che usi le proprietà dell’MCD.
Ricapitolando, dimostreremo per assurdo l’irrazionalità di radice di 2 supponendo che, se n ed m sono primi, questa tesi:
sia vera.
In altri termini, posta la seguente
ipotesi: n ed m sono primi fra di loro
e, supponendo vera la seguente
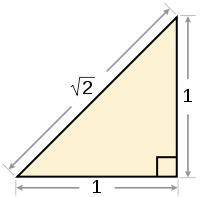
tesi: il loro rapporto è pari a radice di 2
dobbiamo ottenere una contraddizione.
Per le proprietà dell’MCD, sappiamo che se due numeri n ed m sono primi tra di loro, allora
MCD(n,m) = 1
Inoltre, sappiamo che l’MCD dei quadrati di due interi è pari al quadrato del loro MCD:
MCD(n^2, m^2) = MCD(n,m)^2
Applichiamo la nostra ipotesi, per cui MCD(n, m) = 1, e calcoliamo quindi l’MCD tra i quadrati di n ed m:
MCD(n^2, m^2) = MCD(n,m)^2 = 1^2 = 1
Fin qui, abbiamo ottenuto una conseguenza dell’ipotesi per calcolo diretto, cioé che se n ed m sono primi fra di loro, allora anche i loro quadrati sono mutuamente primi.
Ora, la tesi ci dice che il rapporto tra i quadrati di n ed m è pari a 2 e, quindi, applicando le proprietà dell’MCD:
MCD(m^2, n^2) = MCD(m^2, 2 m^2) = MCD(m^2, 2m^2 – m^2) = MCD(m^2, m^2) = m^2
Ovviamente, se n^2 = 2m^2, il massimo comun divisore tra questi due è proprio pari ad m^2. Ed ecco la contraddizione: se supponiamo che il loro rapporto è pari a radice di 2, otteniamo l’opposto dell’ipotesi, e cioé che non sono primi tra di loro.
Ci siamo voluti divertire qui a mostrare come due ferri del mestiere, dimostrazione per assurdo e proprietà dell’MCD, servano perfettamente allo scopo. Ma la cosa più interessante è che la stessa dimostrazione può essere condotta formalmente in molti altri modi !
Non è questo il bello della scienza ?